Get the flag.
bcs.7z
$ nc bcs.chal.ctf.westerns.tokyo 3971
Summary: recovering AES key from partial subkey leaks.
The challenge allows to encrypt any text and to encrypt the flag:
$ ./bcs > encrypt asd Encrypted: 6c4bb9114b4db65c2a0e7043f7693c2d > decrypt asd command not found > flag OK. I'll give you the flag. Encrypted: 97ee6e2e2824906e9f4870553c7b4f49 |
1. Reverse-Engineering
Reversing the binary was pretty easy. The decompiled encryption function:
int __fastcall sub_400B20(const __m128i *a1, const __m128i *a2, __m128i *a3) { ... v3 = a3; v4 = 0LL; v11 = _mm_loadu_si128(a2); _XMM3 = _mm_xor_si128(v11, _mm_loadu_si128(a1)); for ( i = _mm_cvtsi32_si128(1u); ; i = _mm_cvtsi32_si128(dword_400EC0[v4]) ) { __asm { aeskeygenassist xmm0, [rsp+58h+var_58], 0 } v8 = _mm_xor_si128(_mm_srli_si128(_XMM0, 12), v11); v9 = _mm_xor_si128(v8, _mm_slli_si128(v8, 4)); v11 = _mm_xor_si128(_mm_xor_si128(_mm_shuffle_epi32(i, 0), _mm_slli_si128(v9, 8)), v9); if ( dword_6013AC != 322376503 ) break; if ( v4 > 1 ) { v12 = _XMM3; v14 = _mm_load_si128(&v11); v13 = v14; result = printf("%02x%02x", v11.m128i_u8[0], v14.m128i_u8[1], v11.m128i_i64[0]); _XMM3 = _mm_load_si128(&v12); break; } LABEL_3: ++v4; __asm { aesenc xmm3, [rsp+58h+var_58] } if ( v4 == 10 ) goto LABEL_9; } if ( v4 != 9 ) goto LABEL_3; __asm { aesenclast xmm3, [rsp+58h+var_58] } LABEL_9: dword_6013AC = 0; *v3 = _XMM3; return result; } |
It uses AES-NI instructions so most likely it is AES. By debugging the binary and dumping the random key, we can easily verify that it is vanilla AES-128.
Interestingly, the global variable dword_6013AC triggers some leakage (recall the task name). To trigger it, we have to send command l34k1nf0 with value 322376503=0x13371337:
v7 = memcmp(v13, "l34k1nf0 ", 9uLL) == 0; if ( v7 ) { v6 = 0LL; dword_6013AC = strtol(&nptr, 0LL, 10); } |
But what does it leak? It prints the first two bytes of some things, maybe subkeys or intermediate values. Let’s activate it:
$ gdb ./bcs gdb-peda$ b*0x400C7E # calling encryption function Breakpoint 1 at 0x400c7e gdb-peda$ r Starting program: /home/.../bcs > l34k1nf0 322376503 > encrypt 123 Breakpoint 1, 0x0000000000400c7e in ?? () gdb-peda$ x/16xc 0x6013b0 # the global array with random key 0x6013b0: 0x4a 0x93 0x64 0x71 0xf6 0x9d 0x55 0xb3 0x6013b8: 0xf 0x5f 0xc4 0xa5 0x80 0xec 0xef 0x8f gdb-peda$ continue Continuing. ed22d3a6863bb017b97b6bb676dfd003631e849d4c109ee797708d576f4ac457 |
We now know that:
key = 0x4a,0x93,0x64,0x71,0xf6,0x9d,0x55,0xb3,0xf,0x5f,0xc4,0xa5,0x80,0xec,0xef,0x8f leak = ed22d3a6863bb017b97b6bb676dfd003 enc("123") = 631e849d4c109ee797708d576f4ac457 |
Here’s the full expanded key (source code):
plaintext: 31 32 33 00 00 00 00 00 00 00 00 00 00 00 00 00 roundkey 0: 4a 93 64 71 f6 9d 55 b3 0f 5f c4 a5 80 ec ef 8f roundkey 1: 85 4c 17 bc 73 d1 42 0f 7c 8e 86 aa fc 62 69 25 roundkey 2: 2d b5 28 0c 5e 64 6a 03 22 ea ec a9 de 88 85 8c roundkey 3: ed 22 4c 11 b3 46 26 12 91 ac ca bb 4f 24 4f 37 roundkey 4: d3 a6 d6 95 60 e0 f0 87 f1 4c 3a 3c be 68 75 0b roundkey 5: 86 3b fd 3b e6 db 0d bc 17 97 37 80 a9 ff 42 8b roundkey 6: b0 17 c0 e8 56 cc cd 54 41 5b fa d4 e8 a4 b8 5f roundkey 7: b9 7b 0f 73 ef b7 c2 27 ae ec 38 f3 46 48 80 ac roundkey 8: 6b b6 9e 29 84 01 5c 0e 2a ed 64 fd 6c a5 e4 51 roundkey 9: 76 df 4f 79 f2 de 13 77 d8 33 77 8a b4 96 93 db roundkey 10: d0 03 f6 f4 22 dd e5 83 fa ee 92 09 4e 78 01 d2 roundkey 11: 00 7f 43 db 22 a2 a6 58 d8 4c 34 51 96 34 35 83 roundkey 12: c0 e9 af 4b e2 4b 09 13 3a 07 3d 42 ac 33 08 c1 roundkey 13: a8 d9 d7 da 4a 92 de c9 70 95 e3 8b dc a6 eb 4a roundkey 14: c1 30 01 5c 8b a2 df 95 fb 37 3c 1e 27 91 d7 54 roundkey 15: da 3e 21 90 51 9c fe 05 aa ab c2 1b 8d 3a 15 4f ciphertext: 63 1e 84 9d 4c 10 9e e7 97 70 8d 57 6f 4a c4 57 |
Clearly, the leak contains first two bytes from subkeys for rounds 3-10 inclusive.
2. Attempt with z3
Let’s first try to use z3py to solve it. We can use code from Belluminar’s ahyes challenge solution as a basis:
from z3.z3 import * from aes import AES AES = AES() s = Solver() # make AES sbox z3-friendly sbox = AES.sbox[::] AES.sbox = Array("sbox", BitVecSort(8), BitVecSort(8)) for x in xrange(256): s.add(AES.sbox[x] == sbox[x]) # symbolical key expansion almost for free :) master = [BitVec("master%d" % i, 8) for i in xrange(16)] exp = AES.expandKey(master, 16, 11*16) leak = "ed22d3a6863bb017b97b6bb676dfd003".decode("hex") leaks = map(ord, leak) for i in xrange(0, len(leaks), 2): a, b = leaks[i:i+2] s.add(exp[(3+i/2)*16+0] == a) s.add(exp[(3+i/2)*16+1] == b) print s.check() key = "" model = s.model() for m in master: key += chr(model[m].as_long()) print key.encode("hex") |
Running the script and it immediately spits out the key: 4a0820f57cd5983afb70581b22ec324f. However, it is the wrong key (though few bytes match). By iterating over solutions we can see that there are many, around 2^32. For z3 it is a lot to iterate. So we have to figure out the structure of those solutions by ourselves.
3. AES-128 Key Schedule
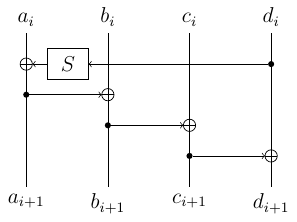
The AES-128 key schedule works as follows: $subkey[0]=(a_0,b_0,c_0,d_0)$ is the master key, and all the consequent subkeys are obtained by applying iteratively the following function:
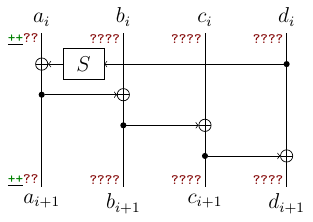
Here $a,b,c,d$ are 32-bit words (think of them as 4 bytes), $S$ applies four 8-bit S-Boxes in parallel and rotates the word by 8 bits. Here is what we know from the leak (“+” are known bytes, “?” – unknown):
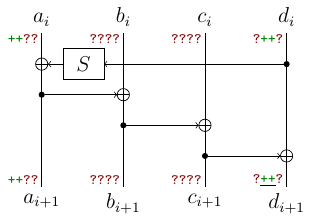
Note that we have leakage for 8 subkeys and the situation from picture occurs only 7 times (both $a_i$ and $a_{i+1}$ are leaked). This number will reduce in a funny way. Now let’s compute other bytes:
- the output of $S$ is equal to $a_i \oplus a_{i+1}$.
- by inverting $S$ we learn two middle (remember rotation) bytes of $d_i$.
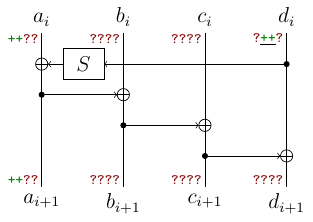
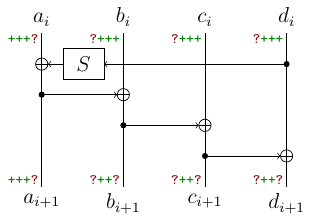
By applying the same thing at next two rounds, we obtain $d_{i+1}$ too. Note that these reduces the number of positions and now we only have 6 such positions.
By continuing these simple computations we obtain that for $i = 8$ we know 12/16 subkey bytes.
Here are all computations:
# d[i] = S^-1[a[i] ^ a[i+1]] for i in reversed(xrange(3, 10)): known[i][13] = isbox[known[i+1][0] ^ known[i][0] ^ rcon[i+1]] known[i][14] = isbox[known[i+1][1] ^ known[i][1]] # c[i+1] = d[i] ^ d[i+1] for i in reversed(xrange(4, 10)): known[i][10] = known[i][14] ^ known[i-1][14] known[i][9] = known[i][13] ^ known[i-1][13] # b[i+1] = c[i] ^ c[i+1] for i in reversed(xrange(5, 10)): known[i][6] = known[i][10] ^ known[i-1][10] known[i][5] = known[i][9] ^ known[i-1][9] # a[i+1] = b[i] ^ b[i+1] for i in reversed(xrange(6, 10)): known[i][2] = known[i][6] ^ known[i-1][6] # reusing same equations but for different bytes # d[i] = S^-1[a[i] ^ a[i+1]] for i in reversed(xrange(7, 10)): known[i-1][15] = isbox[known[i][2] ^ known[i-1][2]] # c[i+1] = d[i] ^ d[i+1] for i in reversed(xrange(7, 9)): known[i][11] = known[i][15] ^ known[i-1][15] # b[i+1] = c[i] ^ c[i+1] for i in reversed(xrange(8, 9)): known[i][7] = known[i][11] ^ known[i-1][11] for i, k in enumerate(known): s = "".join("+" if x is not None else "?" for x in k) print "%2d" % i, s, "%d/16" % s.count("+") |
The result:
0 ???????????????? 0/16 1 ???????????????? 0/16 2 ???????????????? 0/16 3 ++???????????++? 4/16 4 ++???????++??++? 6/16 5 ++???++??++??++? 8/16 6 +++??++??++??+++ 10/16 7 +++??++??+++?+++ 11/16 8 +++??+++?+++?+++ 12/16 9 +++??++??++??++? 9/16 10 ++?????????????? 2/16 |
It is quite interesting that in the end we arrived at 12/16 bytes known only for one subkey (#8). It happened because at each step the first and last subkeys did not have good neighbours. That is, if the backdoor would have leaked 2 bytes for subkeys 0-2, we would have known some almost full subkey. And it seems that with one round less leak the problem would become much harder.
Anyway, we can now bruteforce the 4 unknown bytes of the 8th subkey, revert the AES key schedule, compute the master key and verify it against the known encryption.
We again reuse the Belluminar’s ahyes implementation in C, here’s the main code (full code):
void undo_key_schedule(uint8_t subkeys[11][16]) { uint8_t tmp[4]; for(int i = 8; i >= 1; i--) { FORN(j, 4) subkeys[i-1][12+j] = subkeys[i][12+j] ^ subkeys[i][8+j]; FORN(j, 4) subkeys[i-1][8+j] = subkeys[i][8+j] ^ subkeys[i][4+j]; FORN(j, 4) subkeys[i-1][4+j] = subkeys[i][4+j] ^ subkeys[i][j]; tmp[0] = sbox[subkeys[i-1][12+1]] ^ fexp2(i-1); tmp[1] = sbox[subkeys[i-1][12+2]]; tmp[2] = sbox[subkeys[i-1][12+3]]; tmp[3] = sbox[subkeys[i-1][12+0]]; FORN(j, 4) subkeys[i-1][j] = subkeys[i][j] ^ tmp[j]; } } int main(int argc, char *argv[]) { uint8_t src[16] = "123"; uint8_t dst[16] = {}; uint8_t ciphertext[16] = "\xe2\xa7\x3d\xd0\xd1\x3f\x83\x54\x49\xeb\x3a\x5b\x65\xe7\x08\xb1"; int subkey8[16] = {0xaa,0x42,0x29,-1,-1,0xa4,0x4c,0x86,-1,0xac,0x4a,0x7d,-1,0x81,0x4b,0x19}; int indices[4] = {}; int ni = 0; uint8_t subkeys[11][16]; FORN(i, 16) { if (subkey8[i] == -1) indices[ni++] = i; subkeys[8][i] = subkey8[i]; } for(uint64_t vals = (atoi(argv[1])*1ll) << 24; vals < 1ll << 32; vals++) { if ((vals & 0xffffff) == 0) fprintf(stderr, "%08llx\n", vals); FORN(i, 4) subkeys[8][indices[i]] = (vals >> (i*8)) & 0xff; undo_key_schedule(subkeys); encrypt(dst, src, 16, subkeys[0], 0, 10); if (!memcmp(dst, ciphertext, 16)) { printf("FOUND! %08llx\n", vals); FORN(i, 16) printf("%02x ", subkeys[0][i]); puts(""); } } return 0; } |
In roughly an hour we obtain the correct master key and decrypt the flag: TWCTF{Why_doesn’t_he_leak_the_key_directly}