Boston Key Party CTF 2016 – GCM (Crypto 9pts)

[8] : gsilvis counting magic – 9 – 4 solves : crypto: Here’s a verification/decryption server: gcm.ctf.bostonkey.party:32768 . Get the GCM MAC key (the thing the server prints out on startup). We’ve given you one valid ciphertext to get you started. It has iv: [102 97 110 116 97 115 116 105 99 32 105 118] and tag: [119 179]
gcm-task.tar

Summary: breaking AES-GCM with 2-byte tag

In this challenge we have access to AES-GCM decryption oracle. Our goal is to recover $H = AES_K(0)$. This value is used in the GCM routines.

AES-GCM is authenticated cipher. It means that decrypting modified ciphertexts yields no information except that the ciphertext is incorrect. In GCM authentication is guaranteed by appending a tag to the ciphertext. The tag depends on IV, key, plaintext and possibly additional authentication data. In this challenge tag length is very short: 2 bytes, which makes forgeries possible. Since our goal is to recover some intermediate value of GCM decryption, we will use oracle to find correct tags for our specially crafted ciphertexts by trial. This will leak us about 16 bits of information. Note that to find each tag we need roughly $2^{16}$ queries.

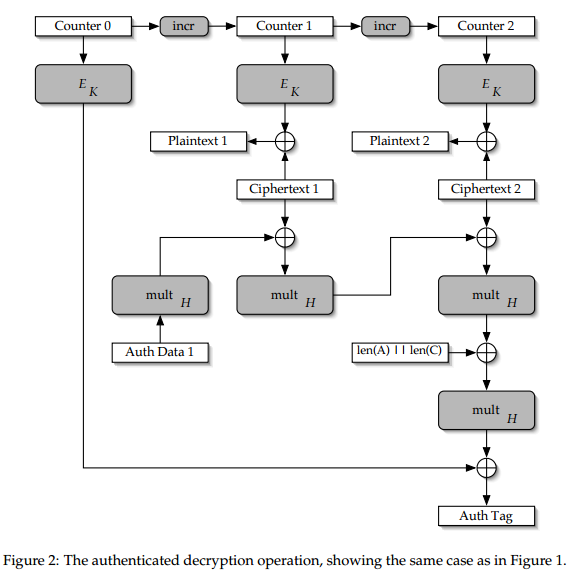
The AES-GCM decryption scheme:

$mult_H$ is multiplication in $GF(2^{128})$ defined by irreducible polynomial $X^{128} + X^7 + X^2 + X^1 + 1$ in little endian bit order.

Let’s consider one-block ciphertexts and fix everything except the block itself. Let the block value be $C$. Then the tag has the following form:

$$T(C) = MSB_{16}\left[ ((f(A) + C) \times H + g(len(A), len(C))) \times H + E_k(IV || 0) \right] =$$
$$ = MSB_{16}\left[ C\times H^2 + t \right],$$

where $f, g$ are some functions and $t$ is some value which does not depend on value of $C$ (but depends on the length); all operations are done in the finite field. Consider the following differential:

$$T(C) + T(C + \Delta) = MSB_{16}(\Delta \times H^2)$$.

Thus, we can recover 16 most significant bits of $\Delta \times H^2$ for arbitrary $\Delta$. Note that multiplication by a constant in finite field is linear and can be written as multiplication by a binary matrix. Therefore we obtain 16 linear equations because of truncation. If we obtain enough equations, we will be able to recover $H^2$ and then recover $H$ by exponentiation.

The algorithm is as follows:

• Fix $C = 0$.
• Obtain several tags $T(C + \Delta)$ for random $\Delta$.
• Construct the system of linear equations and solve it.
• Recover $H$.

Here’s Sage code:

from sage.all import *
 
def s2n(s):
    if not len(s):
        return 0
    return int(s.encode("hex"), 16)
 
def tobin(x, n):
    x = Integer(x)
    nbits = x.nbits()
    assert nbits <= n
    return [0] * (n - nbits) + x.bits()[::-1]
 
def frombin(v):
    return int("".join(map(str, v)), 2 )
 
 
def mat_from_linear_func(m, n, func):
    mat = matrix(GF(2), n, m)
    for i, e in enumerate(reversed(range(m))):
        x = 1 << e
        res = tobin(func(x), n)
        mat.set_column(i, res)
    return mat
 
X = GF(2).polynomial_ring().gen()
poly = X**128 + X**7 + X**2 + X**1 + 1
F = GF(2**128, name='a', modulus=poly)
 
def toF(x):
    # Little endian, so need bit reverse
    x = frombin(tobin(x, 128)[::-1])
    return F.fetch_int(x)
 
def fromF(x):
    # Little endian, so need bit reverse
    x = x.integer_representation()
    x = frombin(tobin(x, 128)[::-1])
    return x
 
def field_mult(a, b):
    return fromF(toF(a) * toF(b))
 
# tags obtained by trial queries to the decryption oracle
texts = [
    "66616e74617374696320697600000000000000000000000000000000e1e9",
    "66616e7461737469632069764d5c97eb7c1db17c26802261d8a0f8ce0ab6",
    "66616e74617374696320697609c0d6d145e19ca06d6396559e9d28bc6d86",
    "66616e746173746963206976cab6bb9ab23006666338a6b0f10cf77d410b",
    "66616e746173746963206976fb562207bfa33dd32075dacbaa5b8998ec5e",
    "66616e74617374696320697671baa8fb9275320eae9f5bc534d71129a8d0",
    "66616e74617374696320697647f195cfc16961a29cf0e6b51ff34cb2d505",
    "66616e7461737469632069764d5c97eb7c1db17c26802261d8a0f8ce0ab6",
    "66616e746173746963206976661fb2b4a720debaec3054f2641bf6157cb9",
    "66616e7461737469632069766f0367a3863ffed6c6abeb66d133d6136fa7",
    "66616e746173746963206976ad07f9965c4d3397b6f3c7d121b6036e2e92",
]
 
ca_lst = []
 
def blocktag(t):
    return int(t[24:-4], 16), int(t[-4:], 16)
 
b0, t0 = blocktag(texts[0])
for t in texts[1:]:
    block, tag = blocktag(t)
    ca_lst.append((block ^ b0, tag ^ t0))
 
fullmat = matrix(GF(2), 16 * len(ca_lst), 128)
fullvec = vector(GF(2), 16 * len(ca_lst))
for i, (c, a) in enumerate(ca_lst):
    print i, hex(c), hex(a)
    m = mat_from_linear_func(128, 128, lambda x: field_mult(x, c))
 
    fullmat[i*16:i*16+16, :] = m[:16,:]
    fullvec[i*16:i*16+16] = vector(GF(2), tobin(a, 16))
 
print "RANK", fullmat.rank()
sol = fullmat.solve_right(fullvec)
assert fullmat * sol == fullvec
H2 = frombin(sol)
 
# invert squaring
d = inverse_mod(2, 2**128-1)
h = fromF(toF(H2)**d)
print "BKPCTF{%032x}" % h

The flag is BKPCTF{40db7f1b3eecb5ae763b1f125f844793}.