Boston Key Party CTF 2016 – Feistel (Crypto 5pts)

feistel – 5 – 15 solves : crypto: I just made a brand new cipher! Can you recover the key?
52.86.232.163:32785
feistel.go

Summary: slide with a twist attack

In this challenge we have access to an encryption and decryption oracle. The cipher is 48-bit 34-round Feistel Network with 2 alternating keys and simple round function:

func f(key uint32, input uint32) uint32 {
	sum := (key + input) & 0x00FFFFFF
	return ((sum & 0x001FFF) << 11) | ((sum & 0xFFE000) >> 13)
}
 
func encrypt(lkey uint32, rkey uint32, left uint32, right uint32) (uint32, uint32) {
	for i := 0; i < 17; i++ {
		left ^= f(lkey, right)
		right ^= f(rkey, left)
	}
	return left, right
}

Note that the inner cycle body can be alternatively written as two usual Feistel rounds:

    left ^= f(lkey, right)
    left, right = right, left
    left ^= f(rkey, right)
    left, right = right, left

Note that bruteforcing the two 24-bit keys is quite realistic. Here we will describe more clever attack. For such many rounds with a nonlinear round function it’s hard to mount linear or differential attack. There is an attack, which is independent on number of rounds – Slide Attack. Note that straightforward application of this attack is not possible, because there are 2 alternating round keys. However, there are advanced variations of the attack (Advanced Slide Attacks).

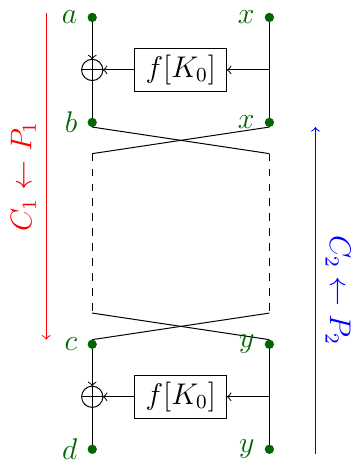
The variation which we will use is called Slide Attack with a Twist. The idea is that when the two keys $k_0, k_1$ are alternating and we do the first round encryption, all the next rounds can be seen as partial decryption: indeed, while decrypting, the round functions use keys $k_1, k_0, k_1, \ldots$ instead of $k_0, k_1, k_0, \ldots$. Thus, a slid pair $(P_1, C_1), (P_2, C_2)$ we are looking for can be described as following:

$$P_1 \xrightarrow{K_0} C_2 \xrightarrow{swap} \xrightarrow{K_1} \ldots \xrightarrow{K_1} \xrightarrow{swap} C_1 \xrightarrow{K_0} P_2$$.

We also need to be careful with swaps.

Let $(a, x) = P_1, (b, x) = C_2, (c, y) = C_1, (d, y) = P_2$. To find a correct slid pair we fix some constant $R$, encrypt $2^{12}$ random plaintexts of form $(?, R)$ and decrypt $2^{12}$ random ciphertexts of the same form. These pools correspond to $P_1$ and $C_2$ respectively (or $C_1$ and $P_2$). Among $2^{24}$ pairs of p/c pairs, by birthday paradox with good probability we will find a pair such that $a \oplus b = f(x)+K_0$ for the correct key $K_0$. If the pair is correct, then the same must hold for another side: $c \oplus d = f(y)+K_0$. Thus, we can filter $2^{24}$ pairs quickly and find a correct slid pair. Such slid pair will yield the correct $K_0$. We can then bruteforce $K_1$.

Here’s the code:

Script for collecting pairs using gevent
Sample of collected pairs (~11000 pairs).

from itertools import *
from random import randint
 
def rol(x, n, bits):
    mask = (1 << bits) - 1
    n %= bits
    x &= mask
    return ((x << n) | (x >> (bits - n))) & mask
 
def split(p):
    l, r = int(p[:6], 16), int(p[6:], 16)
    return l, r
 
spairs = []
for line in open("known.txt"):
    p, c = line.strip().split(":")
    spairs.append((split(p), split(c)))
 
print "Known:", len(spairs)
 
def f(c, k):
    res = (c + k) & 0x00FFFFFF
    return rol(res, 11, 24)
 
def f_extract_key(res, inp):
    res = rol(res, 13, 24)
    return (res - inp) & 0x00FFFFFF
 
def encrypt(k0, k1, l, r):
    for i in range(17):
        l ^= f(k0, r)
        l, r = r, l
        l ^= f(k1, r)
        l, r = r, l
    return l, r
 
for ((a, x), (c, y)), ((d, y2), (b, x2)) in combinations(spairs, r=2):
    if x != x2:
        continue
    if y != y2:
        continue
 
    ktop = f_extract_key(a ^ b, x)
    kbot = f_extract_key(c ^ d, y)
    if ktop != kbot:
        continue
 
    print "Candidate K0", hex(ktop)
    k0 = ktop
    for k1 in xrange(1 << 24):
        for p, c in spairs[:10]:
            ct = encrypt(k0, k1, p[0], p[1])
            if c != ct:
                break
        else:
            print "Flag BKPCTF{%06x%06x}" % (k0, k1)
            quit()

The flag is BKPCTF{32dfa57b9ef0}.