0CTF 2016 Quals – Equation (Crypto 2 pts)

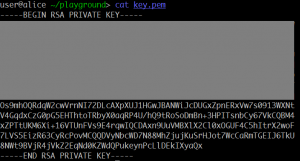
Here is a RSA private key with its upper part masked. Can your recover the private key and decrypt the file?

equation.zip

Summary: recovering RSA key from part of the private key.

In the picture we see a part of a private RSA key. By using some OCR tool and fixing errors, we can obtain the text. We can replace a part of a valid key by this, and use openssl to parse the information. As a result, we see that the following parts are leaked:

prime2:
    *:d2:cf:66:84:e4:
    11:76:a5:b6:73:05:6b:9c:d2:3b:d8:32:dc:01:7a:
    57:50:9d:47:1b
exponent1:
    00:d5:a2:25:c0:d4:1b:16:69:9c:44:71:57:0e:ec:
    d3:dd:77:59:73:6d:57:81:aa:77:10:b3:1b:4a:46:
    e4:41:d3:86:da:13:45:bc:97:d1:aa:91:3f:85:3f:
    85:0f:6d:46:84:a8:0e:60:67:fb:71:cf:21:3b:27:
    6c:2c:ba:ed:59
exponent2:
    13:38:c5:93:d3:b5:42:8c:e9:78:be:d7:a5:53:52:
    71:55:b3:d1:38:ae:ac:08:40:20:c0:c6:7f:54:b9:
    53:01:5e:55:f6:0a:5d:31:38:65:05:e0:2e:61:22:
    da:d7:db:0a:05:ec:b5:52:e4:48:b3:47:ad:c2:c9:
    17:0f:a2:f3
coefficient:
    00:d5:c8:d6:dc:58:3e:cd:f3:c3:21:66:3b:a3:2a:
    e4:ab:1c:9a:2d:ed:67:02:69:19:93:18:42:09:e9:
    39:14:f0:d5:ad:f4:15:63:47:88:d5:91:9d:84:a8:
    d7:74:29:95:9d:40:fb:a4:7b:29:cf:70:b9:43:12:
    42:17:c9:a4:31

So if $n = pq$, $e$ and $d$ are public and private exponents respectively, then we know:

• 200 least significant bits of $p$ (less then half, Coppersmith attack does not work).
• $d_p = d \mod{p-1}$.
• $d_q = d \mod{q-1}$.
• $q_i \equiv q^{-1} \mod{p}$.

Since we know LSBs of $p$, we can try to use the equations modulo $2^{200}$:

$$d_p e \equiv 1 + k_p(p-1) \pmod{2^{200}},$$

$$d_q e \equiv 1 + k_q(q-1) \pmod{2^{200}},$$

where $k_p$ and $k_q$ are some integers. Note that $k_q = (d_q e – 1) / (q-1)$ and $d_q < q-1$. Therefore $k_q \le e$. Assuming $e = 65537$ (default exponent), we have few candidates for $k_q$. We can use the equation modulo $2^{200}$ to check the candidates:

q = 0x3acf6684e41176a5b673056b9cd23bd832dc017a57509d471b
dp = 0x00d5a225c0d41b16699c4471570eecd3dd7759736d5781aa7710b31b4a46e441d386da1345bc97d1aa913f853f850f6d4684a80e6067fb71cf213b276c2cbaed59
dq = 0x1338c593d3b5428ce978bed7a553527155b3d138aeac084020c0c67f54b953015e55f60a5d31386505e02e6122dad7db0a05ecb552e448b347adc2c9170fa2f3
q_inv_mod_p = 0x00d5c8d6dc583ecdf3c321663ba32ae4ab1c9a2ded6702691993184209e93914f0d5adf415634788d5919d84a8d77429959d40fba47b29cf70b943124217c9a431
 
e = 0x10001
mod2 = 2**200
 
for kq in xrange(e):
    if (dq * e) % mod2 == (1 + kq * (q - 1)) % mod2:
        print "Good", kq
        break

We immediately get $k_q = 5277$. Then we can recover $q$: $(q-1) = (d_q e – 1) / k_q$.

Now we need to recover $p$. Let’s use the “coefficient”:

$$q q_i = 1 + k p,$$

where $k$ is some integer. Therefore we can get $kp$ as $kp = q q_i – 1$. To remove $k$, we can use the relation $a^{e d_p} \equiv a \pmod{p}$: we will compute $gcd$ of $kp$ with $a^{e d_p} – a$ which is some multiple of $p$, for different random $a$:

cp = q_inv_mod_p * q - 1
for a in range(5, 1000):
    cp = gcd(cp, pow(a, e * dp, cp) - a)
print "cp =", cp

Not all the factors are removed, but the only factor left is 10, so $cp / 10$ is prime and is actually the prime $p$.

Having $p$ and $q$, we can easily extract the flag:

from libnum import *
 
n = p * q
 
c = s2n(open("flag.enc").read())
d = invmod(e, (p-1)*(q-1))
m = pow(c, d, n)
print `n2s(m)`

Result:

'\x02\xf6\xd0K\xd4\x9e\xa1\xf4\x90f\xc0z\xb9\xa4d^5\x04\x9e*\xda\xeb\xec\xf5
\xa6h\\\x88\xd1\x19\x8d\xdf\x13\xc8\x9f\x9e3\xea}\x90v?\xc7n\xc0\xe5\xf8j\x0b
\xca\xb4\x11\xa6!EF\xb1~\xed\x13\x11K:\x03/6\xc0\x08!\x1b<\x92\x1a}=
\x9a&\x000ctf{Keep_ca1m_and_s01ve_the_RSA_Eeeequati0n!!!}\n'

Note the PKCSv1.5 random padding. The flag is: 0ctf{Keep_ca1m_and_s01ve_the_RSA_Eeeequati0n!!!}