Crypto 500
file
Summary: breaking cipher
This crypto challenge consisted of a service, which allowed encryption of any data using some 64-bit block cipher.
Before encrypting we are given a simple puzzle (find a message with given prefix which SHA1 hash ends with FFFF – solution).
Our aim is to decrypt a given ciphertext. The most straightforward way is to obtain the key and then simply use the decrypt function.
This means we need to break the cipher.
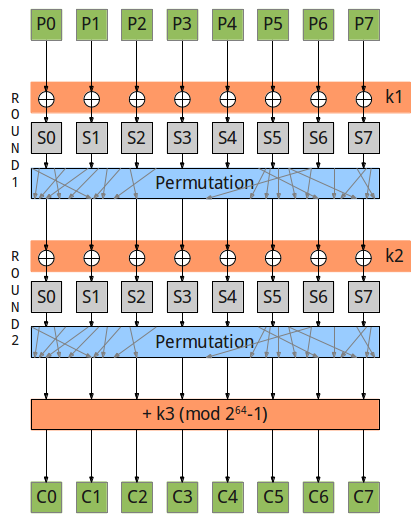
Here’s the cipher scheme:
We can divide it into 3 rounds, first two are similar: xor with round key, substitute with sboxes, permutate. The third one is simply adding the third round key to the data modulo 18446744073709551615. Note that all sboxes are equal (they use the same table).
Let’s look relations between first and second rounds’ sboxes and also between round-3 bits and round-2 sboxes.
(I use another bit ordering – order of bits in a bitstring)
Print for each round-2 sbox, which sboxes from round-1 affect it SBOX 0 : (1, 2, 3, 3, 6, 7, 7, 7) bits: (61, 18, 62, 57, 26, 27, 13, 49) SBOX 1 : (0, 1, 2, 2, 5, 6, 6, 7) bits: (45, 53, 16, 23, 14, 1, 60, 48) SBOX 2 : (0, 0, 1, 3, 4, 4, 4, 5) bits: (0, 44, 39, 36, 3, 15, 28, 34) SBOX 3 : (1, 1, 3, 3, 3, 4, 4, 6) bits: (10, 38, 25, 32, 29, 24, 55, 11) SBOX 4 : (2, 3, 4, 5, 5, 6, 6, 6) bits: (33, 21, 50, 52, 46, 30, 54, 41) SBOX 5 : (0, 0, 0, 1, 4, 6, 7, 7) bits: (4, 58, 35, 51, 6, 5, 63, 9) SBOX 6 : (0, 0, 1, 2, 2, 3, 5, 7) bits: (59, 8, 31, 19, 7, 17, 2, 47) SBOX 7 : (1, 2, 2, 4, 5, 5, 5, 7) bits: (43, 37, 56, 12, 20, 42, 40, 22) Print for each round-3 input bit, which sboxes from round-2 affect it 7 2 7 7 3 3 1 6 5 6 2 2 1 0 7 6 0 5 4 4 0 1 3 4 1 4 3 4 3 3 6 1 4 2 6 6 5 3 6 5 0 7 4 6 0 0 7 1 7 1 3 2 0 2 0 5 5 4 7 1 2 5 5 2 |
For example, SBOX #6 depends on 2 bits from SBOX #0, 1 bit from SBOX #1, 2 bits from SBOX #2, and one bit from each of SBOX #3,#5,#7.
And the last bit of round-3 input depends on round-2 sbox #2.
We can see bits are quite mixed with each other and we can’t easily split the problem into smaller parts, like bruteforcing byte-by-byte.
I also tried linear cryptanalysis (sbox_linear.py):
the best linear approximations for sbox differ from 0.5 only for 0.0625 (there are 1275 such equations though) (in comparison, some DES sbox has difference 0.2).
This small difference still can be used, because there are only three rounds and we can get lots of plaintext/ciphertext pairs.
But managing with this probabilistic method is not that interesting.
Let’s use some other tricks.
The idea is to manipulate the plaintext to trigger the smaller change of the ciphertexts.
Let’s look on some round-1 sbox. If we can craft two such inputs, that outputs differ only in one bit, then only 1 bit in round-2 input will change and therefore only one round-2 sbox output will change (not in 1 bit though). (we can’t craft such inputs directly because of xor k1).
If we have two ciphertexts, how can we check if round-2 output changes only in 1 sbox? (8 bits before round-3)
Let’s say some sbox affects (after permutation) this round-3 input bits:
When adding two numbers, flipping bits in some places can affect not only this places in result, but some higher bits too (because of the carry). The modulus here is interesting too: if the sum is greater or equal than 0xffffffffffffffff, then this number will be subtracted from the sum (because sum of the two numbers which are smaller than modulo can’t exceed modulo*2). And subtraction of 0xff..ff is equal to +1! So the highest carry bit simply goes to the beginning.
Thus we can implement the check – if the differences on ciphertext occur only in bits affected by that sbox or in a line after them – than probably we triggered that one-bit change!
After that we are done: we make a guess for one of byte k1 and try to trigger one-bit changes. If we’ve made right guess, our check will success. If the guess is wrong – after some encryptions we’ll fail a check. In such a way we can get all the k1 bytes.
k2 is even simplier: we make a guess and try to trigger one-bit change in round-2. If we’ve made right guess, only 1 bit in round-3 input will be affected – that’s even easier to check.
k3 is straightforward – we simply subtract the ciphertext (as a number) and a round-3 input.
Here’s the code.
KEY 1 [176, 81, 32, 97, 107, 173, 68, 206] KEY 2 [239, 226, 82, 4, 61, 102, 235, 46] KEY 3 [181, 44, 163, 245, 170, 211, 112, 53] KEY : {HateTSA} |
The flag is: “HateTSA“